The Challenge:
- We are given an n by n checkerboard, in which every square can be one of four distinct colors.
- The goal is to arrange the colors on the checkerboard such that no two adjacent squares have the same color, considering only row-wise and column-wise adjacency (not diagonal).
- This repository accomplishes this task using a genetic algorithm.
Code Explanation
This Python script uses a genetic algorithm to arrange four different colors on an 8 by 8 checkerboard in such a way that no two adjacent squares (row-wise and column-wise, not diagonally) have the same color.
Here is a walkthrough of the code:
- Parameters: error, size, samples, numberOfColors are used to control the checkerboard's size, the number of samples, the number of colors, and to track errors. An initial population is created with populations, a 4x8x8 list of lists where each element is a random number between 0 and numberOfColors.
- printList3d to print a 3D list.
- saveAsImages to save checkerboards as images with different colors for visualization in drive C inside a folder named geneticAlgorithmImages.
- calculateFitness function computes the fitness of each sample in the population by counting the number of neighboring squares with the same color, a lower count signifies a better fitness.
- The calculateRowWise and calculateColWise functions divide each of the best samples in half (either row-wise or column-wise) and calculate the fitness of these halves.
- The calculateHalfPartFitnessPerEachParent function calls these functions for each of the best samples.
- The selectParent function selects the best two samples as parents for the next generation.
- The crossover function combines the best halves from the best samples to generate new samples. It includes row-wise and column-wise combinations.
- The columnWiseCombination function is a helper for the crossover function, used for the column-wise combination.
- The mutation function randomly changes a color in the checkerboard with a 10% probability, introducing variation.
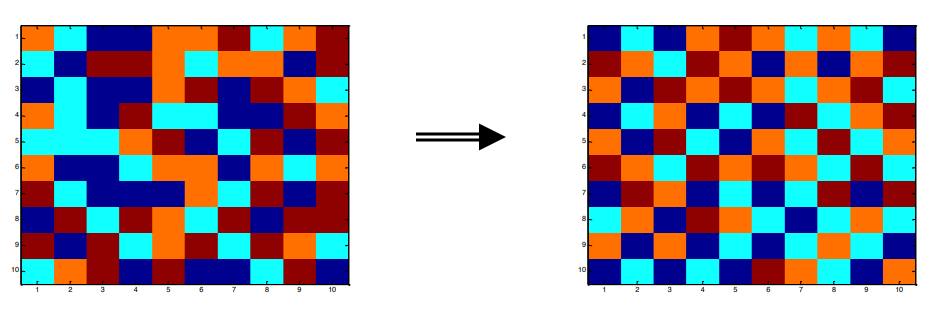
Code output example:
The execution loop in this program continues until it produces an output where no adjacent squares share the same color. The 'output-0.png' file is a guaranteed example of this outcome, as it always follows this rule. However, for the other outputs, such as 'output-1.png', 'output-2.png', and 'output-3.png', this condition may or may not be met. In these cases, there could be instances where adjacent squares still share the same color.
Initial population:
 |  |  |  |
|---|---|---|---|
| input-0.png randomly generated population | input-1.png randomly generated population | input-2.png randomly generated population | input-3.png randomly generated population |
Output popluation:
 |  |  |  |
|---|---|---|---|
| output-0.png guaranteed to have no adjacent squares share the same color | output-1.png may or may not have adjacent squares sharing the same color | output-2.png adjacent squares are more likely to share the same color compared to output-1 | output-3.png adjacent squares are more likely to share the same color compared to output-2 |